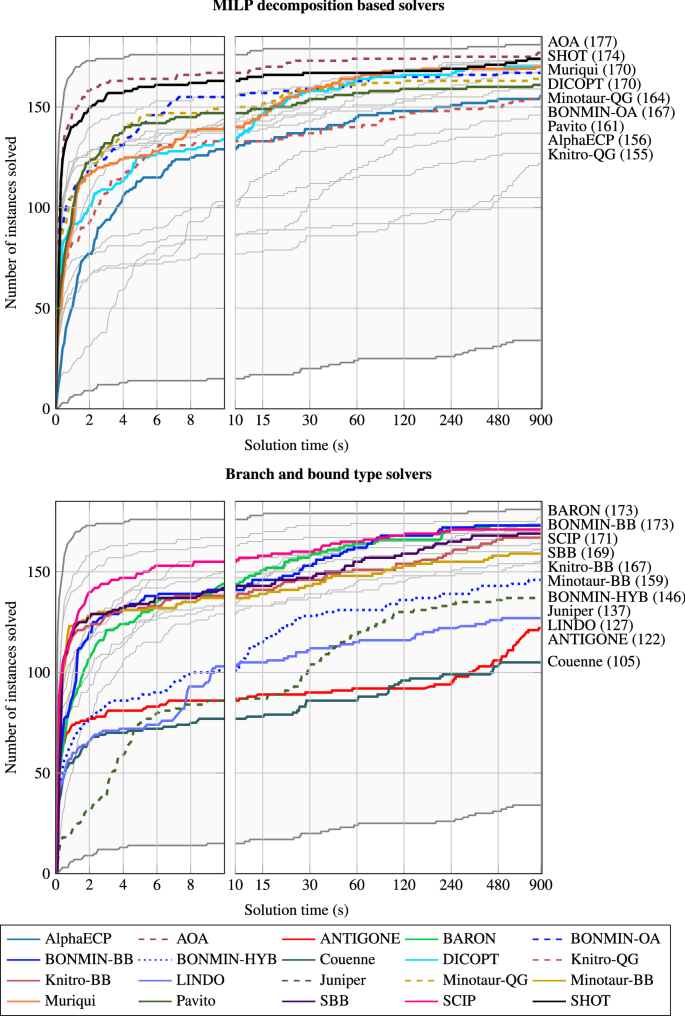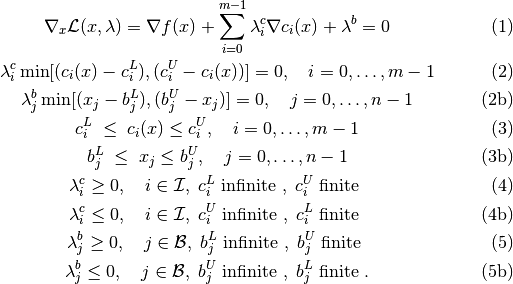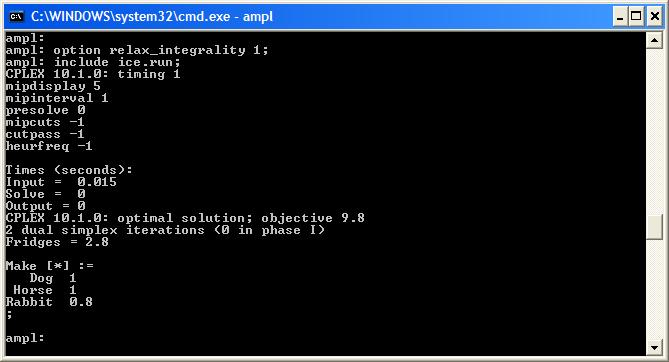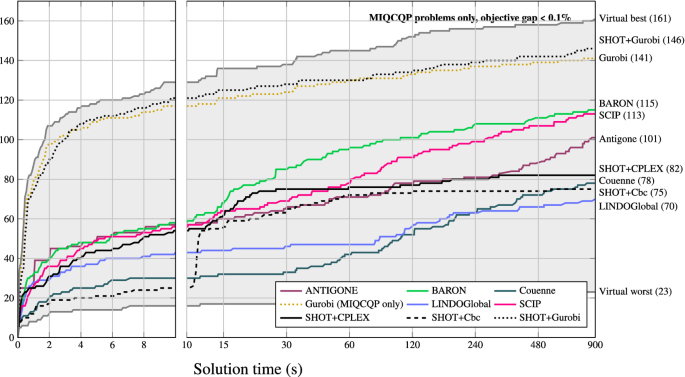
Polyhedral approximation strategies for nonconvex mixed-integer nonlinear programming in SHOT | SpringerLink
Optimality gap and the ratio of simulation time | Download Scientific Diagram
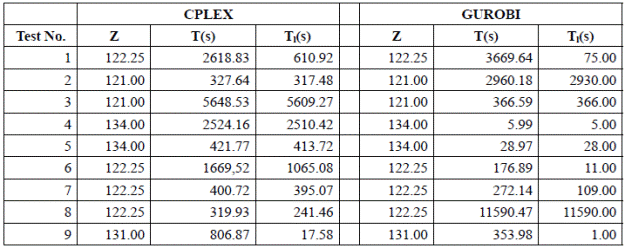
Alinear programming model for the parallel non-related machines problem, in the drying area of a chilean sawmill
A review and comparison of solvers for convex MINLP | SpringerLink
CPLEX 10.1 optimality gap (%) and nodes within the one hour time limit... | Download Table
CPLEX 10.1 optimality gap (%) and nodes within the one hour time limit... | Download Table
Termination criteria — Artelys Knitro 13.0 User's Manual
Comparison in optimality gap with respect to CPLEX for ten random cases... | Download Scientific Diagram
IBM ILOG AMPL CPLEX 12.2 User's Guide
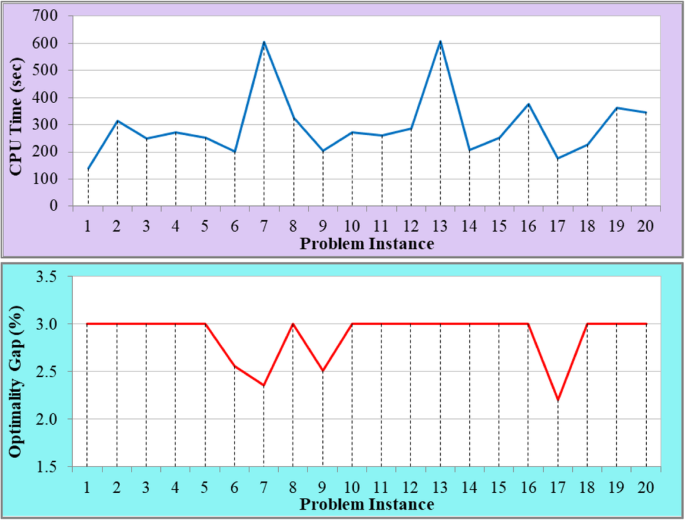
Holistic tactical-level planning in liner shipping: an exact optimization approach | Journal of Shipping and Trade | Full Text
CPLEX Options for AMPL - AMPLAMPL
CPLEX Options for AMPL - AMPLAMPL
Mixed-Integer Programming (MIP) - A Primer on the Basics - Gurobi
Solving your First Problem | Optimisation Intelligence | Octeract
Comparison in optimality gap with respect to CPLEX for ten random cases... | Download Scientific Diagram
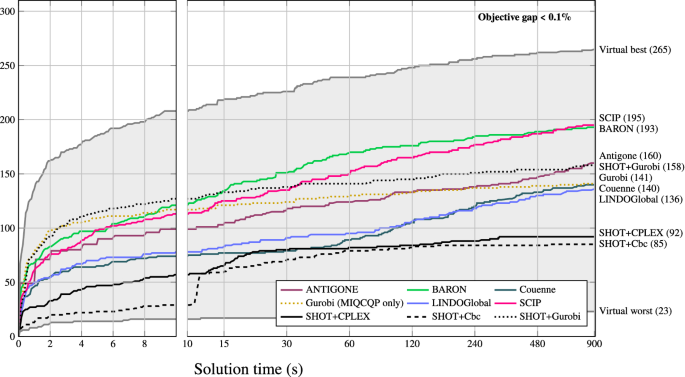
Polyhedral approximation strategies for nonconvex mixed-integer nonlinear programming in SHOT | SpringerLink
Entropy | Free Full-Text | Hierarchical Distribution Matching for Probabilistic Amplitude Shaping | HTML
Routing and scheduling of network flows with deadlines and discrete capacity allocation - Ahani - 2020 - Networks - Wiley Online Library
IntegerProgrammingWithAMPL < OpsRes < TWiki
Objectives
CPLEX Options for AMPL - AMPLAMPL
Attacking Hard Mixed-Integer Optimization Problems Using an - Ampl
Yongjia Song (@songmath) / Twitter
CPLEX 10.1 optimality gap (%) and nodes within the one hour time limit... | Download Table
